Catching the moon at the right time with Julia
The moon on a night sky is surprisingly bright, especially for a camera with limited dynamic range. And there’s only so many compositions one can do of the moon on a naked sky. For those reasons taking moon pictures at sunrise or sunset, when the moon is close to the horizon and its relative brightness is comparable to ambient light often brings more interesting (or at least varied) results.
Maybe I haven’t searched well enough but I haven’t found a tool giving you the days of the year at which moon rise/set coincide with the sun rise/set for a given location. In any case that’s an excuse for a fun Julia project.
Disclaimer: I’m not a physicist or professional astronomer, if you’re planning something critical (like a rocket launch), maybe double-check with actual experts!
The Plan
The idea is simple: find dates when the sun and moon rise or set within a short time window of each other. This gives us those perfect conditions where you get a nicely lit sky and a visible moon. The main functionalities, namely the moon and sun position at a given date, are available via the AstroLib package.
Setup and converting times
First, let’s define where we’re observing from. I’m using Lyon, France as the example location:
using AstroLib, TimeZones
using Dates, Plots
# Location setup: latitude, longitude in degrees
latitude = 45.7640 # Lyon
longitude = 4.8357
obs_altitude = 212
local_tz = TimeZone("Europe/Paris")
start_date = Date(2025, 8, 4)
We also need our timezone to convert between universal time and our local observations.
AstroLib routines take time in Julian days, which surprisingly aren’t Julia specific units,
but units used by astronomers. We can convert from a Julia date
to Julian days with jdcnv :
date_to_jd(date) = jdcnv(DateTime(date))
Computing Altitudes
The get_altitude function is doing the real work here. It takes a Julian date and a position function (sunpos or moonpos), gets the celestial coordinates, and converts them to altitude above our horizon.
When altitude crosses zero, we have a rise or set event.
function get_altitude(jd, posfun=sunpos)
sun_ra_dec = posfun(jd)
sun_alt, sun_az, _ = eq2hor(sun_ra_dec[1], sun_ra_dec[2], jd, latitude, longitude, obs_altitude)
sun_alt
end
The sunpos function returns the right ascension and declination of the Sun at a given date, right ascension and declination being angles defining a direction
on the celestial sphere.
The eq2hor function converts these two angles into an altitude (angle to the horizon) for our local position.
We can make a plot of the altitude for a day. As cou can see on that day the mon rises as the sun is setting, that’s the type of events we are loooking for!
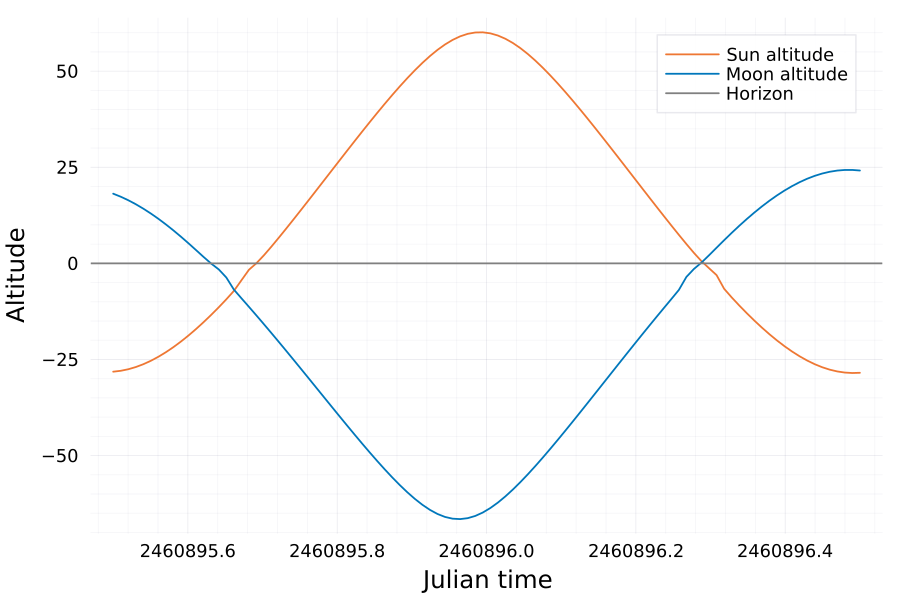
start_date = Date(2025, 8, 8)
jd_start = date_to_jd(start_date)
jd_end = date_to_jd(start_date + Day(1))
t = LinRange(jd_start, jd_end, 100)
p = plot(t, get_altitude.(t, sunpos), label = "Sun altitude", xlabel = "Julian time")
plot!(t, get_altitude.(t, moonpos), label = "Moon altitude", ylabel = "Altitude")
hline!([0], label = "Horizon",c="gray", dpi=150)
Finding the Crossings
To find the horizon crossings I’m using a basic zero-crossing algorithm, with a 1 minute time resolution. I’ve tried root finding with Roots.jl but it surprisingly was getting stuck sometimes. I don’t need more precision anyway.
When altitude goes from negative to positive, that’s a rise. Positive to negative? That’s a set. Simple but effective.
function find_crossing(start_date, num_days, posfun)
jd_start = date_to_jd(start_date)
jd_end = date_to_jd(start_date + Day(num_days))
times = LinRange(jd_start, jd_end, 24*60*num_days) # 1 minute resolution
altitudes = get_altitude.(times, posfun)
crossings = @NamedTuple{time::DateTime, event::Symbol}[]
for i in 2:length(altitudes)
if altitudes[i-1] < 0 && altitudes[i] ≥ 0
push!(crossings, (
time = daycnv(times[i]),
event = :rise,
))
elseif altitudes[i-1] ≥ 0 && altitudes[i] < 0
push!(crossings, (
time = daycnv(times[i]),
event = :set,
))
end
end
crossings
end
The same plot as before with the crossings added :
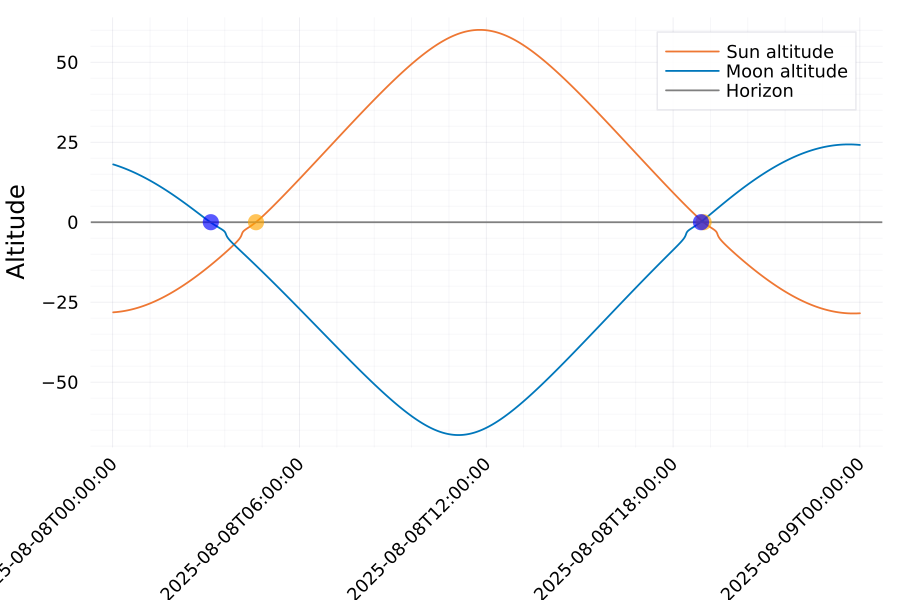
Moon & Sun Coincidences
No need for sophistication either here, we’ll just test every possible pairs of crossing for a year; if they occur within 30 minutes of each other, we keep them.
# Compute crossings for a full year
d = 360
sun_crossings = find_crossing(start_date, d, sunpos)
moon_crossings = find_crossing(start_date, d, moonpos)
# Find coincidences within a 30-minute window
coincidences = Tuple{T,T}[]
for s in sun_crossings
for m in moon_crossings
if abs(s.time - m.time) < Minute(30)
push!(coincidences, (s,m))
end
end
end
Pretty Printing the Results
Finally, let’s format the results nicely, including the moon phase (illuminated fraction) and local times:
| Date | Sun Event | Sun Time | Moon Event | Moon Time | Moon Phase (%) |
|---|---|---|---|---|---|
| 8 Aug, 2025 | sunset | 20h59 | moonrise | 20h53 | 99.6 |
| 9 Aug, 2025 | sunrise | 06h38 | moonset | 06h25 | 99.9 |
| 9 Aug, 2025 | sunset | 20h58 | moonrise | 21h18 | 99.7 |
| 21 Aug, 2025 | sunset | 20h38 | moonset | 20h12 | 2.6 |
| 22 Aug, 2025 | sunset | 20h36 | moonset | 20h35 | 0.3 |
| 23 Aug, 2025 | sunrise | 06h55 | moonrise | 06h46 | 0.0 |
| 23 Aug, 2025 | sunset | 20h35 | moonset | 20h54 | 0.3 |
| 6 Sep, 2025 | sunset | 20h09 | moonrise | 19h42 | 98.6 |
| 7 Sep, 2025 | sunset | 20h07 | moonrise | 20h02 | 100.0 |
| 8 Sep, 2025 | sunset | 20h05 | moonrise | 20h20 | 98.6 |
| 20 Sep, 2025 | sunset | 19h41 | moonset | 19h17 | 1.2 |
| 21 Sep, 2025 | sunset | 19h39 | moonset | 19h33 | 0.0 |
| 22 Sep, 2025 | sunrise | 07h32 | moonrise | 08h00 | 0.2 |
| 22 Sep, 2025 | sunset | 19h38 | moonset | 19h48 | 0.8 |
| 23 Sep, 2025 | sunset | 19h36 | moonset | 20h04 | 3.6 |
| 6 Oct, 2025 | sunset | 19h11 | moonrise | 18h42 | 99.7 |
| 7 Oct, 2025 | sunrise | 07h51 | moonset | 08h10 | 99.9 |
| 7 Oct, 2025 | sunset | 19h09 | moonrise | 19h02 | 99.5 |
| 8 Oct, 2025 | sunset | 19h07 | moonrise | 19h27 | 96.3 |
| 21 Oct, 2025 | sunrise | 08h09 | moonrise | 08h02 | 0.1 |
| 21 Oct, 2025 | sunset | 18h44 | moonset | 18h28 | 0.1 |
| 22 Oct, 2025 | sunset | 18h42 | moonset | 18h49 | 1.4 |
| 5 Nov, 2025 | sunrise | 07h30 | moonset | 07h28 | 99.8 |
| 5 Nov, 2025 | sunset | 17h21 | moonrise | 16h52 | 99.8 |
| 6 Nov, 2025 | sunset | 17h20 | moonrise | 17h28 | 97.9 |
| 20 Nov, 2025 | sunrise | 07h51 | moonrise | 08h12 | 0.2 |
| 20 Nov, 2025 | sunset | 17h04 | moonset | 16h47 | 0.3 |
| 21 Nov, 2025 | sunset | 17h03 | moonset | 17h25 | 1.9 |
| 4 Dec, 2025 | sunrise | 08h09 | moonset | 07h48 | 99.1 |
| 5 Dec, 2025 | sunset | 16h56 | moonrise | 16h57 | 99.1 |
| 19 Dec, 2025 | sunrise | 08h21 | moonrise | 08h09 | 0.7 |
| 20 Dec, 2025 | sunset | 16h58 | moonset | 17h02 | 0.5 |
| 3 Jan, 2026 | sunset | 17h09 | moonrise | 16h57 | 99.8 |
| 18 Jan, 2026 | sunrise | 08h19 | moonrise | 08h22 | 0.4 |
| 18 Jan, 2026 | sunset | 17h27 | moonset | 17h02 | 0.1 |
| 1 Feb, 2026 | sunrise | 08h05 | moonset | 08h07 | 99.4 |
| 16 Feb, 2026 | sunrise | 07h44 | moonrise | 07h20 | 1.7 |
| 17 Feb, 2026 | sunrise | 07h42 | moonrise | 07h43 | 0.1 |
| 17 Feb, 2026 | sunset | 18h10 | moonset | 18h23 | 0.1 |
| 18 Feb, 2026 | sunrise | 07h41 | moonrise | 08h02 | 0.7 |
| 2 Mar, 2026 | sunrise | 07h20 | moonset | 06h59 | 98.2 |
| 3 Mar, 2026 | sunrise | 07h18 | moonset | 07h18 | 99.9 |
| 3 Mar, 2026 | sunset | 18h30 | moonrise | 18h42 | 99.9 |
| 4 Mar, 2026 | sunrise | 07h16 | moonset | 07h36 | 99.3 |
| 18 Mar, 2026 | sunrise | 06h50 | moonrise | 06h24 | 0.9 |
| 18 Mar, 2026 | sunset | 18h51 | moonset | 18h31 | 0.2 |
| 19 Mar, 2026 | sunrise | 06h48 | moonrise | 06h42 | 0.1 |
| 20 Mar, 2026 | sunrise | 06h46 | moonrise | 07h01 | 1.9 |
| 1 Apr, 2026 | sunrise | 07h23 | moonset | 06h58 | 99.2 |
| 1 Apr, 2026 | sunset | 20h09 | moonrise | 19h46 | 99.8 |
| 2 Apr, 2026 | sunrise | 07h21 | moonset | 07h15 | 99.9 |
| 3 Apr, 2026 | sunrise | 07h19 | moonset | 07h33 | 98.6 |
| 18 Apr, 2026 | sunrise | 06h52 | moonrise | 06h49 | 0.9 |
| 1 May, 2026 | sunset | 20h48 | moonrise | 21h00 | 99.8 |
| 2 May, 2026 | sunrise | 06h29 | moonset | 06h22 | 99.6 |
| 3 May, 2026 | sunrise | 06h28 | moonset | 06h50 | 97.8 |
| 16 May, 2026 | sunset | 21h06 | moonset | 21h25 | 0.2 |
| 17 May, 2026 | sunrise | 06h10 | moonrise | 05h53 | 0.4 |
| 30 May, 2026 | sunset | 21h21 | moonrise | 21h04 | 99.5 |
| 1 Jun, 2026 | sunrise | 05h57 | moonset | 06h09 | 99.2 |
| 14 Jun, 2026 | sunset | 21h31 | moonset | 21h37 | 0.3 |
| 15 Jun, 2026 | sunrise | 05h53 | moonrise | 05h26 | 0.2 |
| 29 Jun, 2026 | sunset | 21h34 | moonrise | 21h43 | 99.8 |
| 30 Jun, 2026 | sunrise | 05h57 | moonset | 05h53 | 99.9 |
| 13 Jul, 2026 | sunset | 21h28 | moonset | 21h21 | 0.7 |
| 28 Jul, 2026 | sunset | 21h13 | moonrise | 20h55 | 99.3 |
| 29 Jul, 2026 | sunrise | 06h23 | moonset | 05h54 | 99.8 |
| 29 Jul, 2026 | sunset | 21h12 | moonrise | 21h22 | 99.9 |
We can double check that a full moon will indeed around 17h the 3 Jan, 2026 in Lyon :
https://www.timeanddate.com/moon/france/lyon?month=1&year=2026
Code
You can generate similar tables for your location and timezone. It would be cool to provide an interactive page doing that.
